Zamislite slijedeću situaciju: Policija vas zaustavi, testira na COVID-19 i test pokaže da ste pozitivni. Gotovo svatko od nas bio bi uvjeren, nakon takvog rezultata testiranja, da je zaražen, makar ne imao simptome.
Kolika je stvarna vjerojatnost da ste zaraženi ako ste na test pozitivni?
Račun vjerojatnosti pokazuje da to ovisi o dva faktora. Jedan, očigledan, je pouzdanost testa. Drugi, koji nije tako očigledan, je postotak zaraženih u ukupnoj populaciji iz koje se slučajno bira osoba koja se testira.
S H1 označimo događaj: slučajno odabrana osoba iz ukupne populacije je zaražena. Vjerojatnost tog događaja, označimo ju s P(H1), jednaka je postotku zaraženih u ukupnoj populaciji podijeljenom sa sto. Na primjer u Hrvatskoj je momentana procijena da ima 2000 zaraženih na 4 000 000 stanovnika, dakle 0.5 promila; u tom slučaju P(H1) = 0.0005.
S H2 označimo događaj: slučajno odabrana osoba iz ukupne populacije nije zaražena. U navedenom primjeru P(H2) = 0.9995.
S A+/H1 označimo događaj: ako je slučajno odabrana osoba, koju se testira, zaražena, test će biti pozitivan.
S A-/H1 označimo događaj: ako je slučajno odabrana osoba, koju se testira, zaražena, test će biti negativan.
S A+/H2 označimo događaj: ako slučajno odabrana osoba, koju se testira, nije zaražena, test će biti pozitivan.
S A-/H2 označimo događaj: ako slučajno odabrana osoba, koju se testira, nije zaražena, test će biti negativan.
Da bi test bio pouzdan, vjerojatnosti događaja A+/H2, ako je testirana osoba nezaražena, test će biti pozitivan, i događaja A-/H1, ako je testirana osoba zaražena, test će biti negativan, moraju biti male. Za savršeni test te vjerojatnosti bi bile nula, ali za realan test one su veće od nule.
Vjerojatnost da je test slučajno odabrane osobe pozitivan ako je osoba zaražena, P(A+/H1), nije ista kao vjerojatnost da je slučajno odabrana osoba zaražena ako je test pozitivan, P(H1/A+).
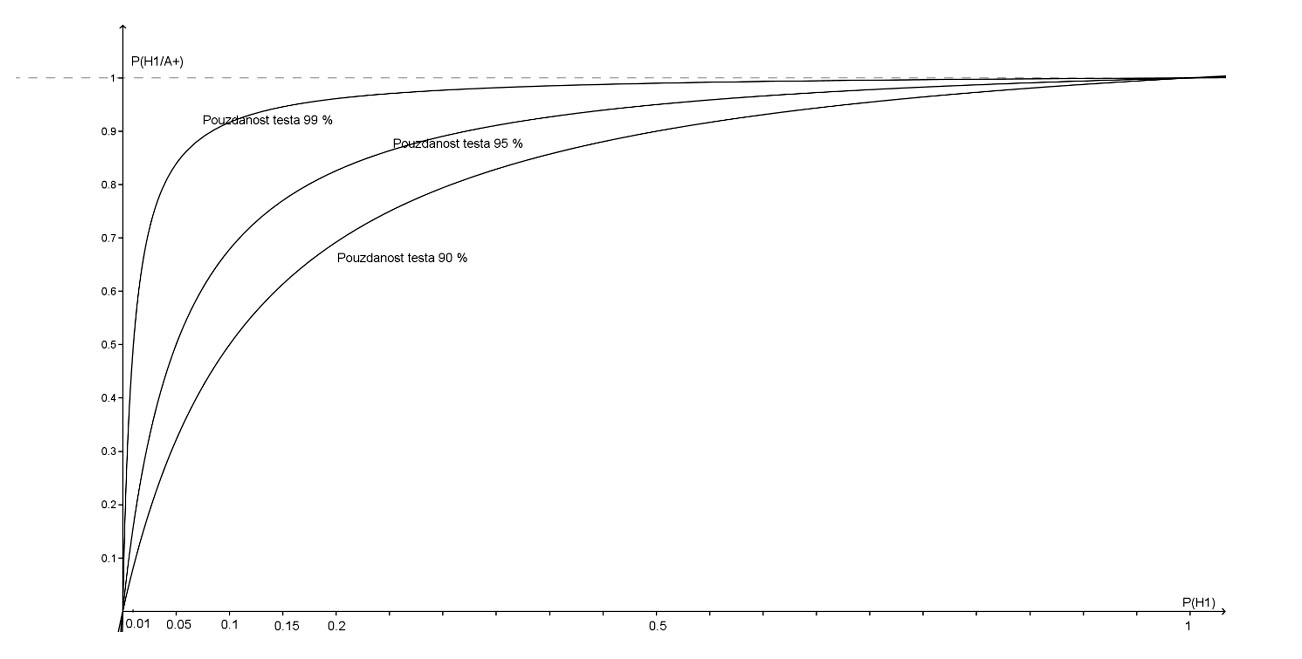
P(A+/H1) govori o pouzdanosti testa; test reagira na neke simptome karakteristične za COVID-19, dakle ako je izabrana osoba iz skupa zaraženih H1. Tri krivulje prikazane na priloženom grafu razlikuju se u pretpostavljenoj pouzdanosti; za jednu krivulju pretpostavljena pouzdanost je 99 %, što znači da je P(A+/H1) = 0.99, za drugu 95 %, za treću 90 %.
Nas ovdje interesira vjerojatnost događaja: ako je slučajno odabrana osoba na test dane pouzdanosti pozitivna, ona je zaražena, P(H1/A+).
Pretpostavljamo da se osoba koja se testira slučajno bira iz populacije u kojoj je skup zaraženih H1, vjerojatnost da je izabrana osoba iz tog skupa je P(H1). P(H1) ovisi o skupu iz kojeg se osoba za testiranje bira; ako se bira među svim građanima pojedine države, P(H1) će, za sada, biti mali, ako se bira iz skupa ljudi koji imaju temperaturu i izgubili su osjećaj mirisa, P(H1) će biti velik.
Krivulje na priloženom grafu pokazuju ovisnost P(H1/A+) o P(H1), dakle, praktički, ovisnost vjerojatnosti da je osoba koju test proglasi pozitivnom uistinu zaražena o postotku zaraženih u skupu iz kojeg osobu za testiranje slučajno biramo.
Račun koji stoji iza priloženog grafa pokazuje da P(H1/A+) bitno ovisi o P(H1), dok je P(A+/H1), pouzdanost testa, o P(H1) neovisna.
Dok je postotak zaraženih u populaciji iz koje se slučajno bira osoba koju se testira, P(H1), mali, biti će i P(H1/A+) mali. To znači da, u tom slučaju, iako je test pozitivan, vjerojatnost da je osoba zaražena je mala. Račun pokazuje da će za pola promila zaraženih u skupu iz kojeg se slučajno bira osoba za testiranje, ta osoba biti zdrava u 95 % slučajeva, iako je na 99% pouzdani test pozitivna. To je kontraintuitivni zaključak.
Za sada to, navodno, vrijedi gotovo u svim zemljama pogođenim zarazom; evidentirani broj zaraženih je u Hrvatskoj oko 0.5 promila, u Italiji oko 3 promila.
Iz računa slijedi da u tom slučaju nema smisla slučajno testiranje na čitavoj populaciji.
Graf, odnosno račun na osnovu kojeg je graf dobiven, pokazuje da vjerojatnost događaja – ako ste pozitivni onda ste i zaraženi, P(H1/A+), brzo raste kako raste postotak zaraženih u populaciji iz koje slučajno biramo osobu koju testiramo. Što je test pouzdaniji, dakle što je P(A+/H1) veće, to će i vjerojatnost P(H1/A+) brže rasti s rastom P(H1). Na primjer, za test s 99% pouzdanošću, P(A+/H1) = 0.99, vjerojatnost da ste zaraženi kad ste na test pozitivni, P(H1/A+), prelazi 0.9 kad postotak zaraženih u populaciji iz koje birate osobu koju testirate, pređe 8 %.
U tom slučaju masovno testiranje ima smisla. Drugim riječima, masovno testiranje ima smisla na skupu ljudi sa simptomima karakterističnim za COVID-19, za njih je P(H1) mnogo veći nego za slučajno odabranu osobu iz skupa svih građana.
Za test s pouzdanošću 90%, vjerojatnost da je slučajno odabrana osoba zaražena ako je na test pozitivna, prelazi = 0.9 tek ako je zaraženo preko 50% populacije.
*Neki moji prijatelji ukazali su mi na tekst Zvonimira Šikića, objavljen na portalu ideje.hr, i zamolili me za matematičko objašnjenje njegovih tvrdnji. Potaknut time izveo sam račun iz kojeg slijde priloženi grafovi. Zaključci koje na osnovu izvedenog računa ovdje iznosim potvrđuju zaključke koje iznosi kolega Šikić.
tacno




